均匀平面天线阵列（UPA）信道在球坐标系下的建模

雪斌

前言

这篇文章主要想说明一下均匀平面天线阵列（UPA）针对远场平面波的信道建模。写这篇文章的原因是，最近在读各种各样关于UPA的通信系统的文章，发现他们都会使用一个相似的方式来描述远场平面波下的UPA信道，并且由此定义一个俯仰角 \phi 和方向角 \theta （具体见第二节）。少不经事的我就天真的以为这两个角就是球坐标系中的两个角度坐标了，结果在很多仿真实践中就出现了许多bug，使本就不多的发量雪上加霜。
在仔细研究了之前文章中的建模后，我发现这两个角度并不是定义在球坐标系下的。虽然在一般的全向天线假设下，这个差别并不会引起仿真结果上的变化，但是如果要考虑天线的方向图的话，这个传统建模就完全不适用了，毕竟天线的方向图一般还是定义在球坐标系下的。因此，在本文中我将介绍传统UPA的建模方式以及其使用的坐标系，并且给出在球坐标系下UPA的信道建模。
传统文章中关于UPA信道的建模及使用坐标系

关于在传统文章中经常使用的UPA信道建模，及其所在的坐标系，之前已经有相关的说明了，
在此拾出其主要内容：

对于一个 P × Q 的UPA天线阵列， 即共有P 行，Q 列天线。 则对于 (\theta,\phi) 方向的响应可以写为（ \theta 为方向角， 被称为 azimuth angle，\phi  为俯仰角，被称为 elevation angle) ：
\mathbf{a}=\mathbf{a}_{y}\otimes\mathbf{a}_{z} ，
其中，
\mathbf{a}_y=\frac{1}{\sqrt{Q}}\left[1,\mathrm{e}^{j\pi\mathrm{sin}\theta\mathrm{sin}\phi},\dots,\mathrm{e}^{j\pi(Q-1)\mathrm{sin}\theta\mathrm{sin}\phi}\right]^T,
\mathbf{a}_z=\frac{1}{\sqrt{P}}\left[1,\mathrm{e}^{j\pi\mathrm{cos}\phi},\dots,\mathrm{e}^{j\pi(P-1)\mathrm{cos}\phi}\right]^T,
其中 \otimes  表示克罗内克积。

到此为止，细心的读者可能已经发现了，这里所使用的角度符号已经和球坐标系中的不同了。对于球坐标系，一般我们使用 \theta  表示俯仰角， \phi 表示方向角，但是在这里却反了过来。这不是因为之前的作者粗心写错了，而是由于UPA特殊的摆放方式导致的，具体内容如下：

事实上， 他基于且必须基于下图中的建模：

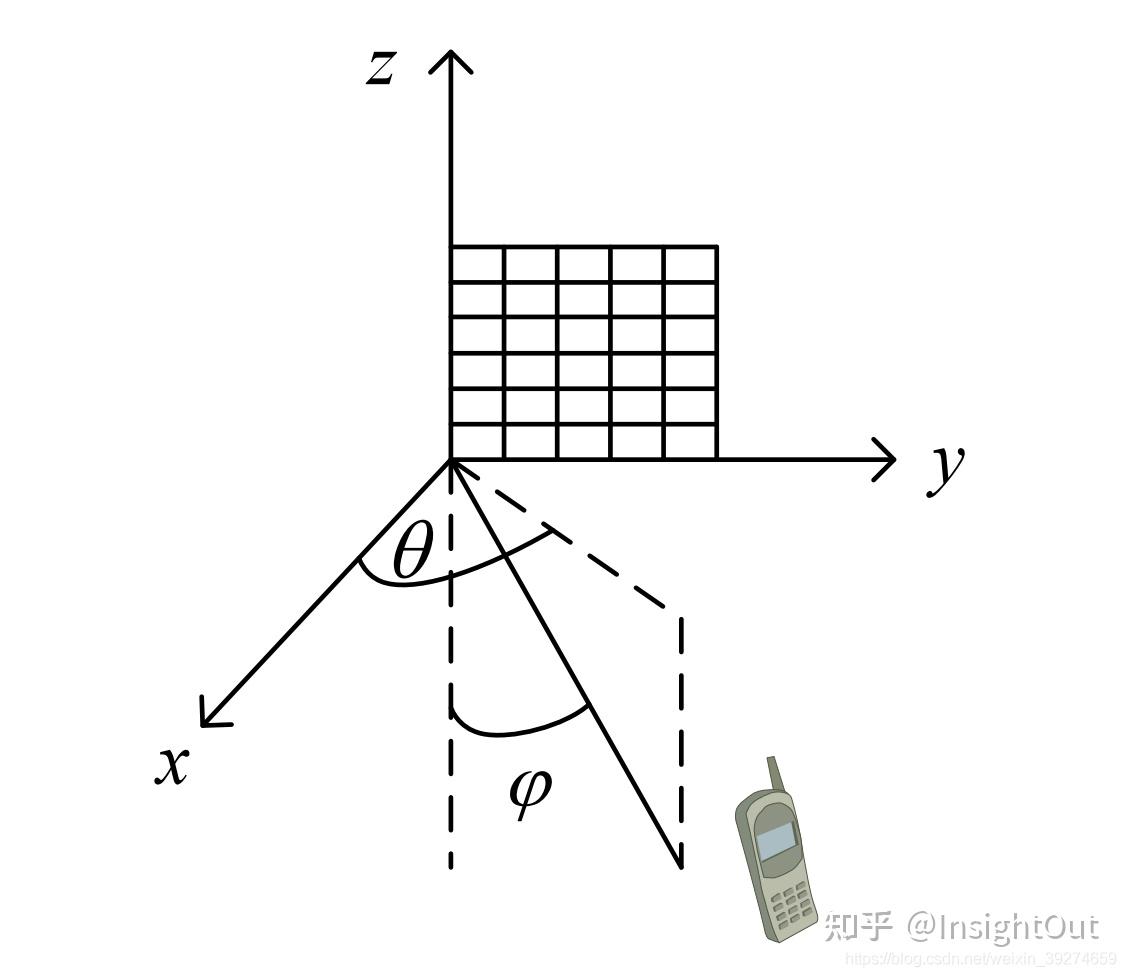
传统UPA信道的建模

如图：
假设UPA建立在yz平面上， 且原点为UPA的左下角第一个元素。
\theta  为用户投影到xy平面后， 与x轴夹角
\phi 为用户与z轴负半轴的夹角

在这个建模中，UPA被放置在了yz平面内，因此与平面法线方向（x轴）之间的夹角 \theta 被定义为了方向角（因为它的定义方式对应于球坐标系下的方向角），而与z轴负半轴之间的夹角 \phi 被定义为了俯仰角。需要说明的是，在这种情况下，即使把UPA转移放置到xy平面内， \theta  也并不对应着球坐标系中的俯仰角。这是因为照此定义，\theta  在此时是用户先投影到xz平面内（对应于转移钱的xy平面），再与z轴的夹角，而不是球坐标系中用户直接与z轴的夹角。因此，如果在这种表示中考虑天线的方向图（一般是球坐标系中俯仰角的函数），大概率就当场去世了。
球坐标系下UPA信道的建模

在清楚了传统UPA远场平面波信道建模的问题之后，我们就可以推导在球坐标系下对应的建模方式了。具体而言，考虑如下图所示的UPA摆放方式



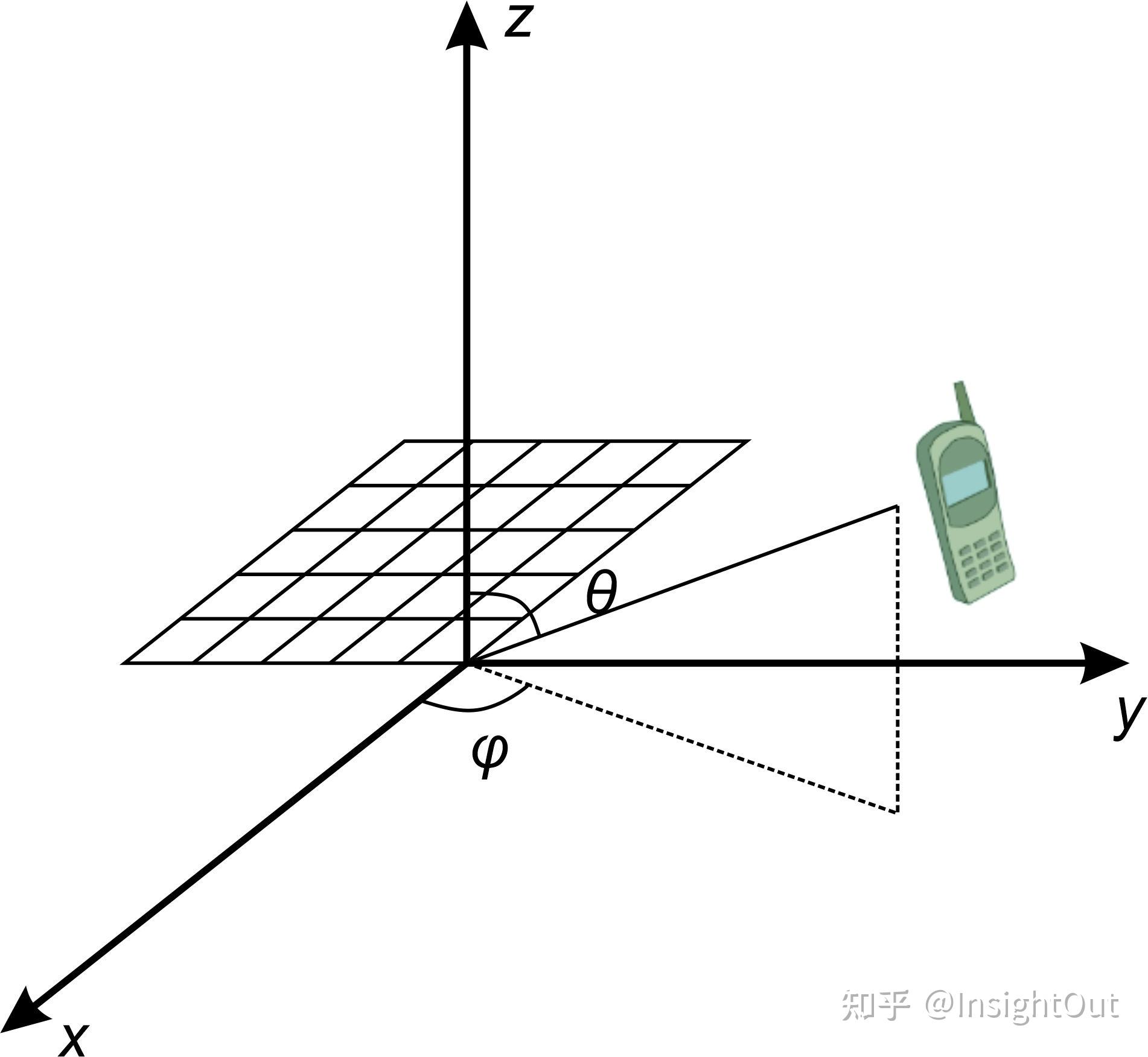
球坐标下UPA信道建模

其中，UPA被放置在xy平面内，左上角的单元被设定为第一个单元。参照球坐标系的要求， \theta  定义为用户与z轴夹角， \phi 定义为用户在xy平面内的投影与x轴正半轴的夹角，此时，UPA信道依旧可以写成类似于传统UPA信道建模的形式，只是其函数需要做如下转换。
\mathbf{a}=\mathbf{a}_{x}\otimes\mathbf{a}_{y},
\mathbf{a}_x=\frac{1}{\sqrt{P}}\left[1,\mathrm{e}^{-j\pi\mathrm{sin}\theta\mathrm{sin}\phi},\dots,\mathrm{e}^{-j\pi(P-1)\mathrm{sin}\theta\mathrm{sin}\phi}\right]^T,
\mathbf{a}_y=\frac{1}{\sqrt{P}}\left[1,\mathrm{e}^{-j\pi\mathrm{sin}\theta\mathrm{cos}\phi},\dots,\mathrm{e}^{-j\pi(P-1)\mathrm{sin}\theta\mathrm{cos}\phi}\right]^T,
如果细心的话，可以发现其对应位置的元素是与球坐标系与笛卡尔坐标系的坐标关系有着千丝万缕的联系的。这个转换过程比较复杂，在这里暂且略去，只举 \theta,\phi\in[0,\frac{\pi}{2}] 的特例来验证这个模型的正确性。此时用户状态就是图中所画的那样，x，y，z坐标都是正的。显然，此时 \theta, \phi 的所有正弦余弦值都是正的，那么由模型可以推出，所有其他用户的相位都相对于左上角的第一个单元提前，意味着其他所有单元距离用户都比第一个单元更近，这也与图中所描绘的情况相同。
以上就是在球坐标系下的UPA信道啦，正如上文所说的，这种建模最大的好处就是和天线方向图的坐标系实现了统一，那么如果要考虑天线的方向图，只要把其方向图与信道简单相乘就可以了，而不用做俯仰角，方向角的转换了（事实上我尝试着转换了一下，转到人麻了也没有转出来，衰）。

真的不是我

very good