声波——三维平面波（下）（未完成）

落日暮年

上篇见：
仅供参考，若有出入，请以南大《声学基础》为准。欢迎指出，我将进行思考和修改。
<hr/>4. 声波方程的解（复习）

4.1 谐波分析下的通解

我们有三维的波动方程： \begin{aligned}\Delta p-\frac{1}{c_0^2}\frac{\partial^2p}{\partial t^2}=0\end{aligned}\tag{5} 其平面波的解为 p(\mathbf{r},t) = Ae^{j(\omega t-\mathbf{k}\cdot\mathbf{r})}+Be^{j(\omega t+\mathbf{k}\cdot\mathbf{r})}\tag{8a} 其中 \mathbf{k}\cdot\mathbf{r} = k_xx+k_yy+k_zz,\;\mathbf{k} = \frac{\omega}{c}\mathbf{n} = k\mathbf{n}\tag{8b}
图9是上述解的直观表达。三维空间里存在一个平面波，其传播方向为 \mathbf{n} （平面的法向量）。这个三维空间的声场为 p(\mathbf{r},t) ，其中 \mathbf{r} 表示空间里任意点 M 的坐标。



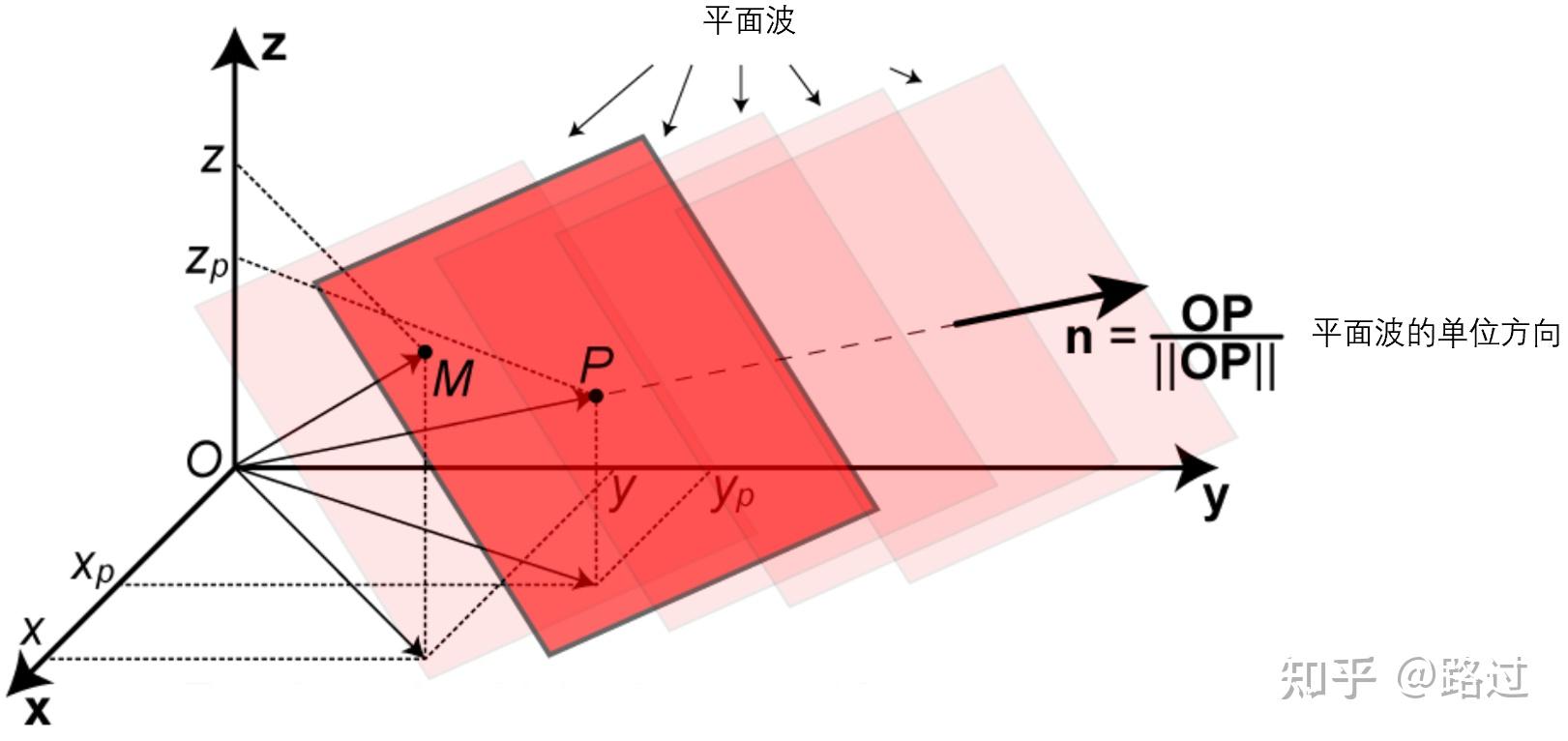
图9. 三维平面波

4.2 声强

声强的三维详细探讨已经在之前的文章给出这里就不再重复。见声波—— 一维平面波（补充篇）第3章。这里直接给出结论 \mathbf{I} = p\mathbf{v} = \frac{1}{4}(\hat{p}\hat{\mathbf{v}}^*+\hat{p}^*\hat{\mathbf{v}})\tag{19}
4.3 波数

以下为2023.02.05截止我个人对波数的理解，仅供参考。
这里解释一下为什么总喜欢谈论波数 |\mathbf{k}| = \frac{\omega}{c} ，其中 \mathbf{k} 的方向是声波的传播方向。
方向：因为一般情况下，我们研究流体介质里的声波。所以声波在这种情况下是纵波，即质点速度 \mathbf{v} 方向和波数 \mathbf{k} 方向相同。
大小：在傅里叶变化中，为了方便研究，我们可以将时间转化为频率 t\leftrightarrow \omega （时域与频域的转换）。同样的如果我们将距离进行傅里叶变换，那么可以得到 x\leftrightarrow k 。这也是为什么会有频散关系dispersion relation研究，即寻找频散曲线 \omega(k) 。

5. 反射与折射

5.1 反射与折射

现在我们分析两个三维流体介质里的反射与折射。



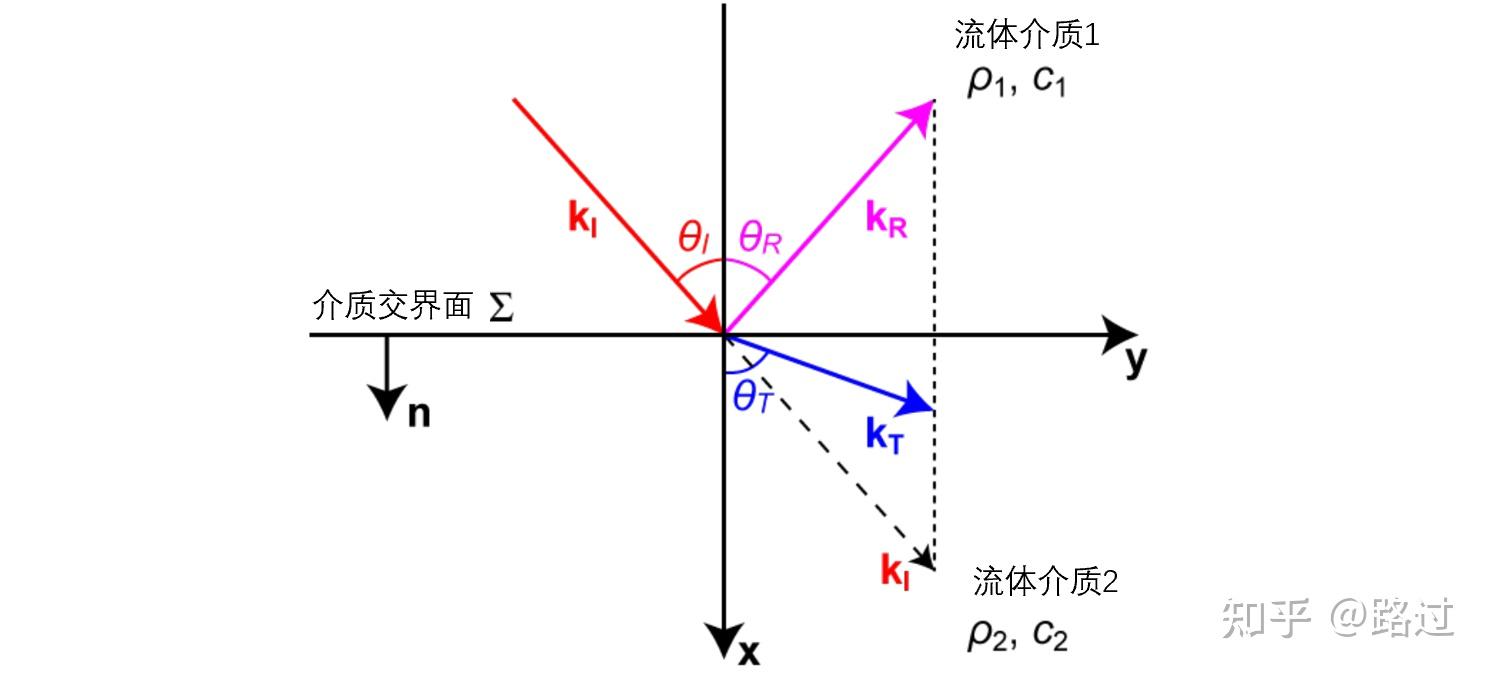
图10. 两个三维流体介质里的反射与折射

根据之前的学习，我们知道流体介质交界处遵循连续定律。即 p_1 = p_2,\;\mathbf{v}_1\cdot\mathbf{n} = \mathbf{v}_2\cdot\mathbf{n}  。声波—— 一维平面波（补充篇）4.2节。
有同学可能会好奇，为什么速度只在平面法线方向连续，而不在切线方向连续，或者直接整个速度都连续。这是因为，我们不考虑流体的粘滞阻力。在有剪切力时，理想流体是可以无限形变的。所以切线方向的速度可以不连续。（参考利用光的粒子性解释斯涅尔定律）
因为在流体介质时，波数方向和质点速度方向相同。所以可以写出声波的折射定律Snell's law \mathbf{k}_I\sin\theta_I=\mathbf{k}_R\sin\theta_R = \mathbf{k}_T\sin\theta_T\tag{20}
很多时候，为了方便表示这个关系，使用圆进行画图，见图11。



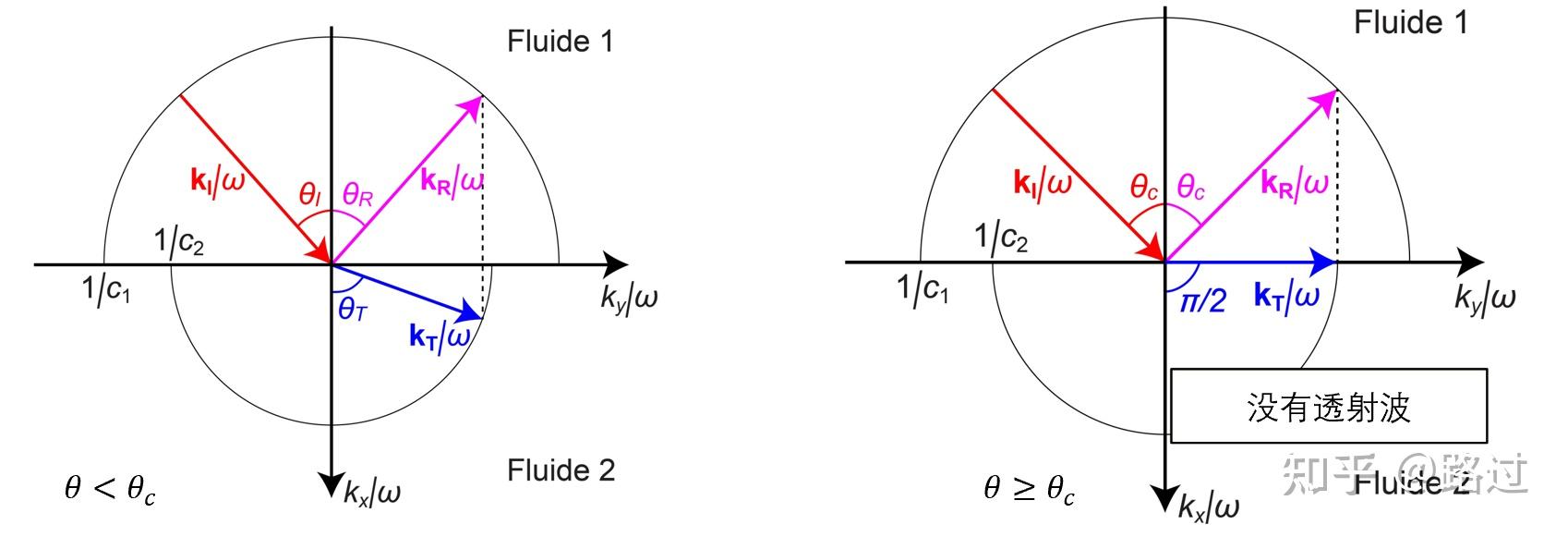
图11. 声波的折射定律Snell's law

根据折射关系（20）或图11可得，当 c_2>c_1 时，存在一个临界角 \theta_c ： \sin\theta_c = \frac{c_1}{c_2}\tag{21} 使得入射角大于临界角 \theta>\theta_c 时，没有透射波。
但是此时真的一点“波”都没有么（压强恒为零）？见下节。
5.2 临界角与隐失波evancescent

现在我们计算两个三维流体介质里的反射与折射，见图10。
在介质1里的声场为 p_1(x,y,t) = A_i e^{j(\omega t-k_1\sin\theta_1 y)}[e^{-jk_1\cos\theta_1x}+R_pe^{jk_1\cos\theta_1x}]\tag{22a} 且在介质2里的声场为 p_2(x,y,t) = A_i e^{j(\omega t-k_1\sin\theta_1 y)}T_pe^{-jk_2\cos\theta_2x}\tag{22b} 根据欧拉方程（1），我们可以得到 x 分量的速度为 \begin{align} v_x^1 &= \frac{\cos\theta_1}{Z_{c1}}A_ie^{j(\omega t-k_1\sin\theta_1y)}[e^{-jk_1\cos\theta_1x}-R_pe^{jk_1\cos\theta_1x}]\\ v_x^2 &= \frac{\cos\theta_2}{Z_{c2}}A_ie^{j(\omega t-k_1\sin\theta_1y)}T_pe^{-jk_2\cos\theta_2x} \end{align} \tag{23} 其中 Z_{c1} = \rho_1c_1,Z_{c2}=\rho_2c_2 是介质的特征阻抗。
运用在 x=0 处的连续性，即 \begin{align} p_1(x=0,y,t) &= p_2(x=0,y,t)\\ v_x^1(x=0,y,t) &= v_x^2(x=0,y,t) \end{align}\tag{24} 所以可以得到 \begin{align} R_p &= \frac{Z_{c2}\cos\theta_1-Z_{c1}\cos\theta_2}{Z_{c2}\cos\theta_1+Z_{c1}\cos\theta_2}\\ T_p &= \frac{2Z_{c2}\cos\theta_1}{Z_{c2}\cos\theta_1+Z_{c1}\cos\theta_2} \end{align}\tag{25}
当 \theta_i=0 时，即变为一维。见声波—— 一维平面波（下）。这里就不再重复讨论。
现在我们分析临界角与隐失波。

• 当 c_1>c_2 时，没有临界角。
  
• 当 c_1<c_2 时，有临界角，其值为 \sin\theta_c = {c_1}/{c_2} 。
  

如果 \theta_i\leq\theta_c ，有透射波。但如果 \theta_i>\theta_c 时，我们来分析介质2里的声场。 \cos^2\theta_2 =1-\sin^2\theta_1 = 1- \frac{c_2^2}{c_1^2}\sin^2\theta_1<0\\ 所以可以得到 \cos\theta_2 = -j\sqrt{\frac{c_2^2}{c_1^2}\sin^2\theta_1-1}\tag{26} 因为波不会随着传播而增强，所以符号“ + ”没有物理意义。代入可得 R_p = e^{2j\arctan{\frac{b}{a}}}\tag{27} 其中 a = Z_{c2}\cos\theta_1,b=Z_{c1}\sqrt{\frac{c_2^2}{c_1^2}\sin^2\theta_1-1} 。
对其取绝对值可得 |R_p|=1 ，代表的就是没有波全部反射，没有透射。虽然相位的变化会引起隐失波，但隐失波并不会传播，见图13和图14。



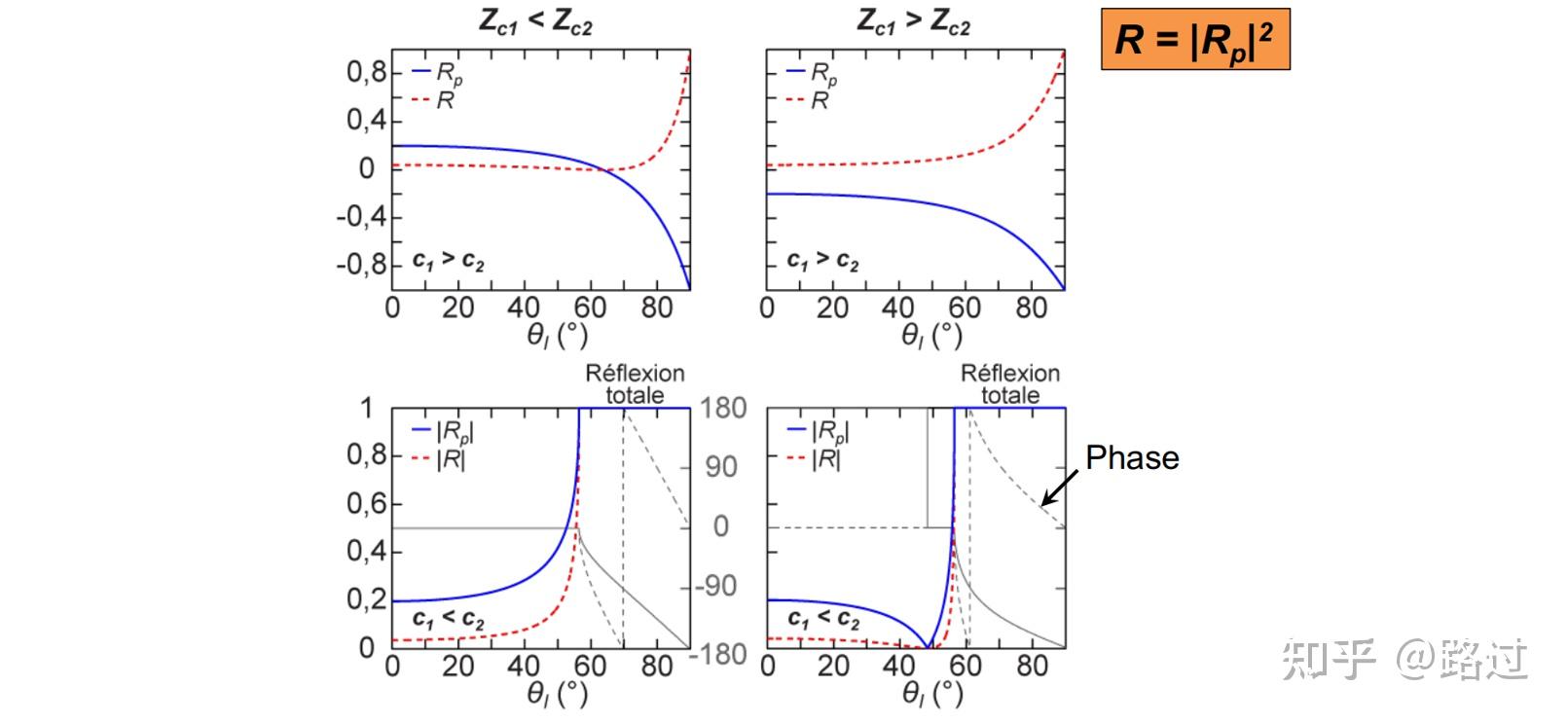
图12. 反射系数



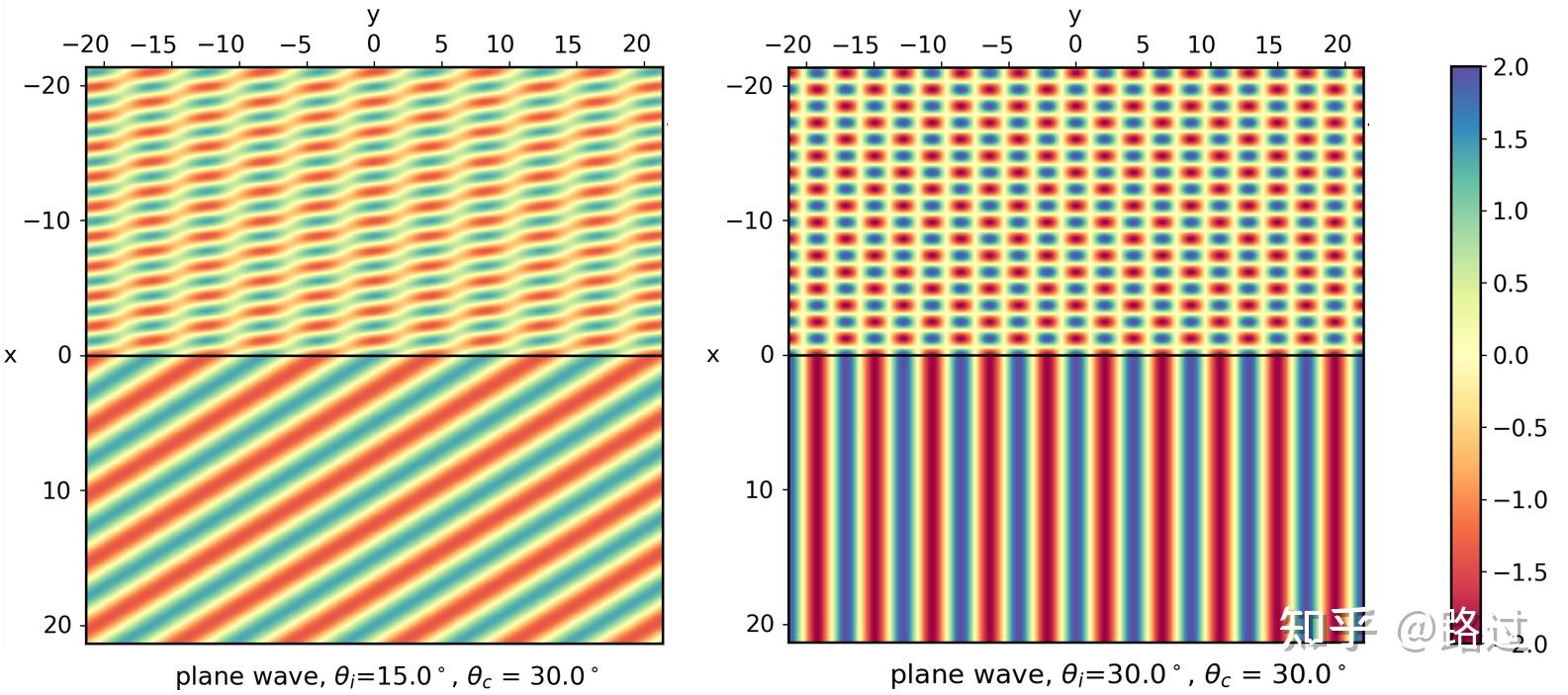
图13. 透射



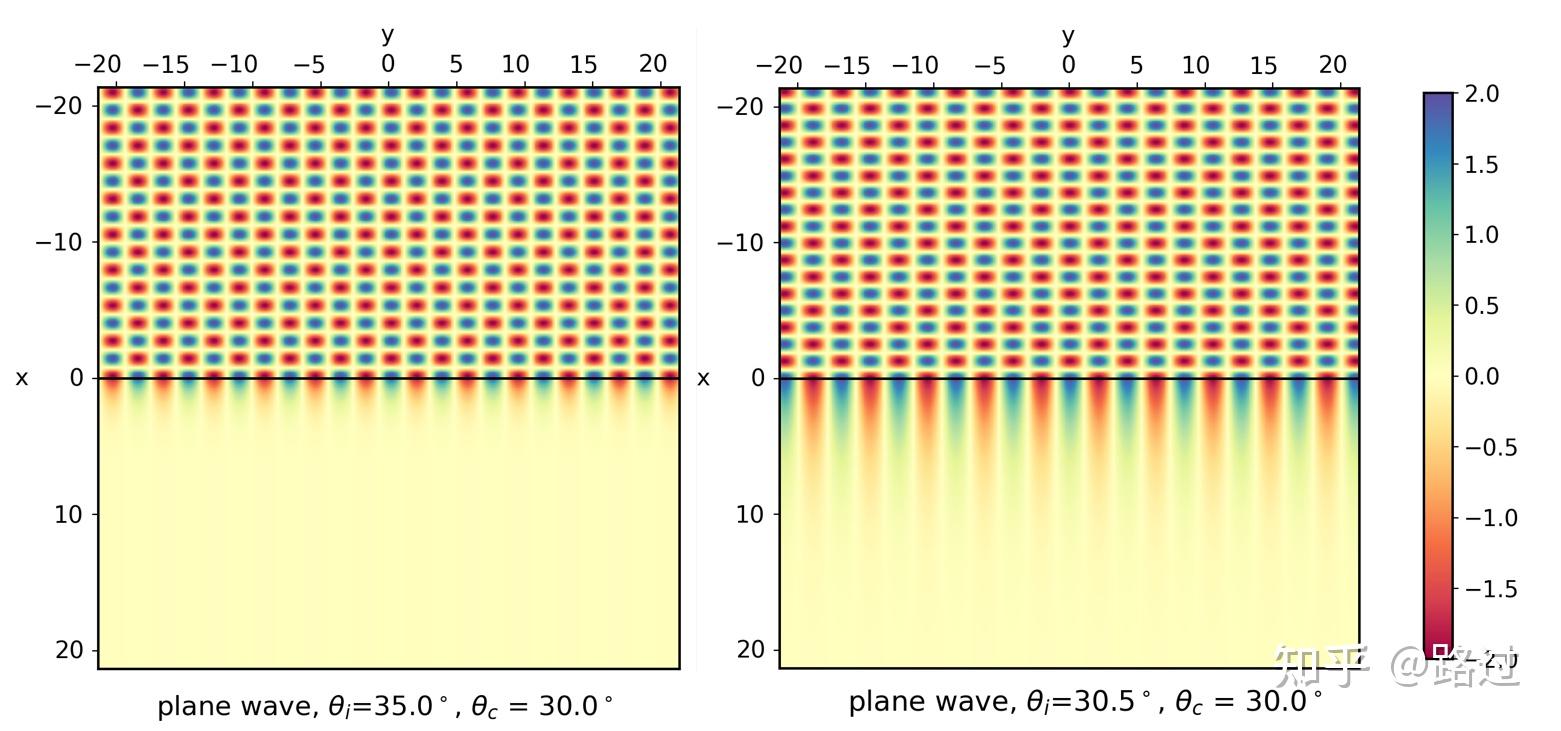
图14. 隐失波evancescent

5.3 声强

现在我们计算一下 x 方向的声强。
\begin{align} I_x^1&= \frac{1}{4}(\hat{p}_1{\hat{v}_x^1}^*+\hat{p}_1^*{\hat{v}_x^1}) = \frac{A_1^2\cos\theta_1}{2Z_{c1}}(1-|R_p|^2)\\ I_x^2&= \frac{1}{4}(\hat{p}_2{\hat{v}_x^2}^*+\hat{p}_2^*{\hat{v}_x^2}) = \frac{A_1^2}{2Z_{c2}}|T|_p^2Re\{\cos\theta_2\} \end{align}\tag{28} 因此可以知道当 \theta_1>\theta_c 时， Re\{\cos\theta_2\}=0 ，所以 I_x^2=0 ，即没有透射波。

6. 波导

因为上篇路过：声波——三维平面波（上）主要就在介绍波导，所以此处一笔带过，就当是对上篇的复习。
p_{t}(x,y,z,t) = Ae^{j(\omega t-k_zz)}\cos\left(\frac{m\pi}{L_x}x\right)\cos\left(\frac{m\pi}{L_y}y\right)\;其中(m,n)\in \mathcal{Z}\\ 其中模态 (m,n) 的截止频率为 f_c^{(m,n)} = \sqrt{\frac{m^2}{L_x^2}+\frac{n^2}{L_y^2}}\frac{c_0}{2}\\ 低于截止频率的模态不传播。
<hr/>如果觉得对您有用，请点个赞，让更多人需要时能搜到。制作这么多公式和图片的像教材一样的半原创优质文章不易，请多多支持。你的点赞是我继续更新的动力。