|
|
复数还有一种几何标识法,他是借用了地图制图学中将地球投影到平上的测地投影法,复平面上的点与球面上的点一一对应(除了球的极点,后面会引入一个无穷远点来描述他)。
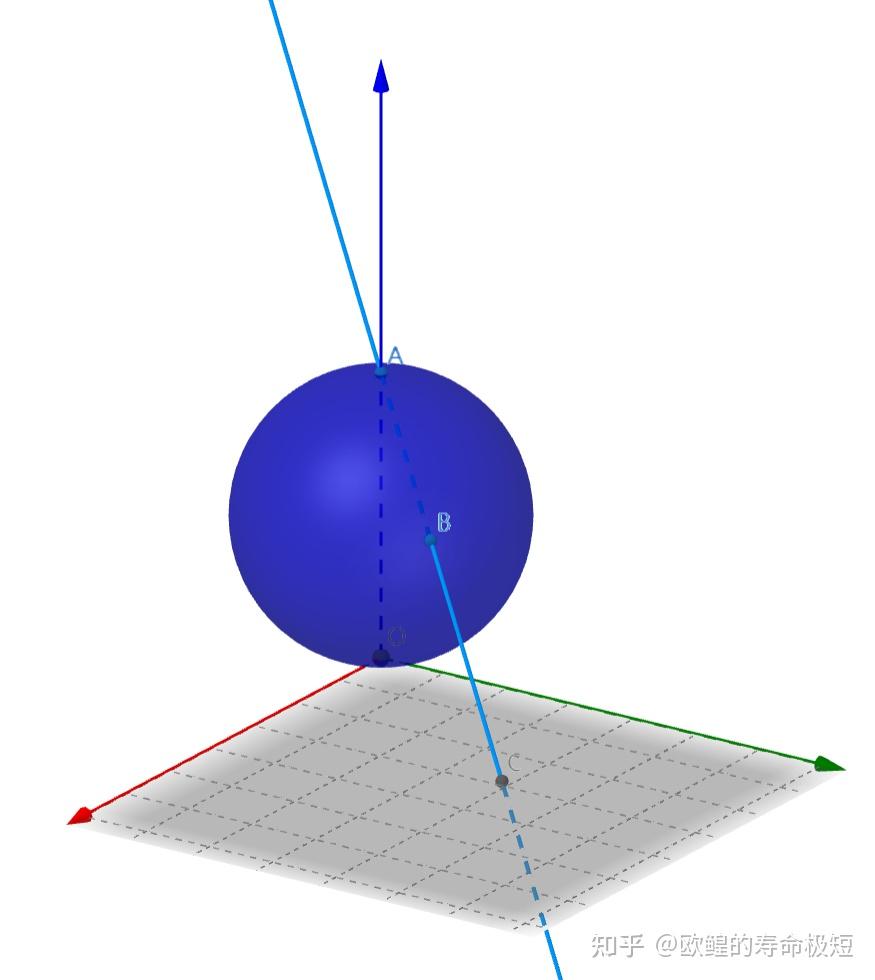
球面上的点通过球极投影到复平面上
取一个在原点O与复平面z相切的球面,通过点O作垂直于z平面的直线与球面交于点A,此时点A被称为球面的北极点,O被称为球面的南极点。在球面上任意选取一点B,通过点A和点B的直线交平面z于点C,这样就将球面上的点投影到了复平面上。球面上除了极点以外的其他点都可以在复平面上找到对应的投影点。
无穷远点的引入
其他球面上的点在复平面上都有了一一对应的点,接下来我们再考虑极点如何描述。如果我们在球面上选择的点恰为极点A,将无法确定唯一的一条穿过复平面的直线。可以想象,当我们在球面上选取的点B慢慢接近极点A,那么他们引出的直线与平面之间的夹角就会越来越小,交点就会落在距离原点更遥远的地方。如果令点B无限的接近于点A,则对应的点将处于无穷远的位置。因此,北极点A可用看作是跟复平面上一个模为无穷大的假想点对应。这个假想点被称为无穷远点,记为∞。复平面加上点∞后被称为扩充复平面,常记作 C_{\infty} , C_{\infty} = C+{\infty} ,与扩充复平面对应的就是整个球面,称为复球面。扩充复平面的一个几何模型就是复球面。
对于新数∞,有以下几点规定:
(1)运算\infty\pm\infty,\infty\cdot0,\frac{\infty}{\infty},\frac{0}{0}均无意义
(2)a\ne\infty时,\frac{\infty}{a}=\infty,\frac{a}{\infty}=\infty,\infty\pm a=a\pm \infty = \infty
(3)b\ne 0(但可为\infty)时,\infty\cdot b = b\cdot\infty=\infty,\frac{b}{0}=\infty
(4)\infty的实部、虚部和辐角均无意义,|\infty| = +\infty
(5)复平面上所有不是简单闭曲线的直线都经过点\infty,没有一个半平面包含点\infty
扩充复平面上的几个概念
1、扩充复平面上,无穷远点的邻域应理解为以原点为圆心的某圆周的外部,即 \infty 的 \varepsilon 邻域 N_\varepsilon(\infty) 是指满足条件 |z|>\frac{1}{\varepsilon} 的点集,它正好对应着复球面上以北极为心的一个球盖。 \infty 的去心邻域是指 \frac{1}{\varepsilon}<|z|<+\infty ,它正好对应去点北极点的一个球盖。在扩充复平面上,聚点、内点和边界点的概念均可推广到点 \infty 。于是复平面以 \infty 为其惟一的边界点;扩充复平面以 \infty 为内点,且它是惟一无边界的区域。
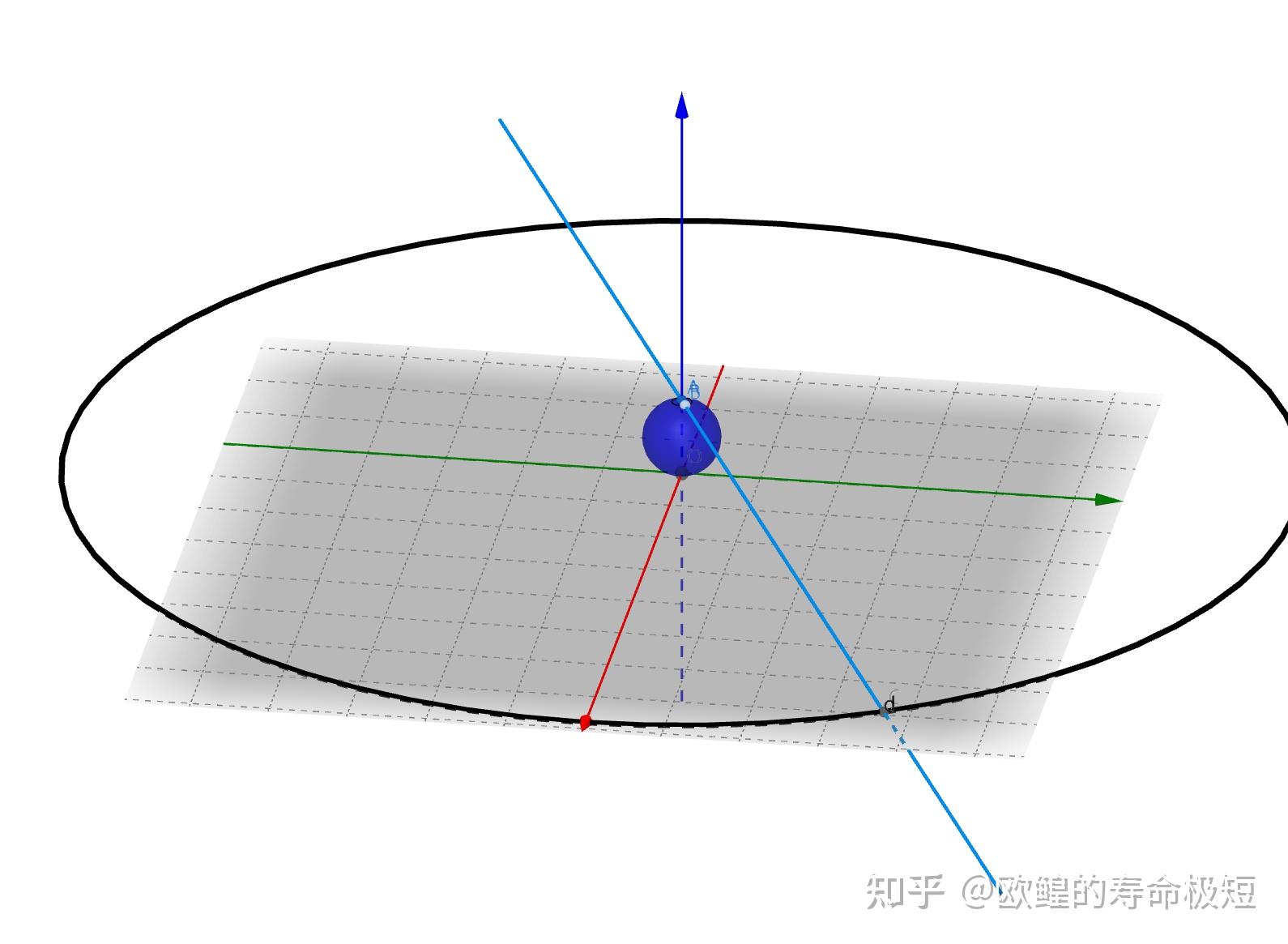
大概是这种感觉,球面上的极点ε邻域的边界在复平面上是一个很大的圆周
2、在扩充复平面中,点 \infty 可以包含在函数的定义域中,函数值也可以取到 \infty ,因此函数的极限与连续性的关系可以有所推广,在关系式\lim_{z \rightarrow z_0}{f(x)}=f(z_0)中,如果 z_0 及 f(z_0) 他们之一或者同时取到 \infty ,则称 f(z) 在 z_0 点是广义连续的,极限就称为广义极限。在这种广义的意义下,极限和连续的 \varepsilon-\delta 说法也应修改为:
任给\varepsilon>0,存在\delta>0,只要有|z|>\frac{1}{\delta},就有|f(z)-f(\infty)|<\varepsilon
投影坐标的表示法
通过投影映射,我们可用把三维球面的坐标信息映射到二维复平面上,假设我们想把一个球心位于 (0,0,\frac{1}{2}) ,半径为 \frac{1}{2} 的圆通过这种方法映射到复平面上。
设球面上一点的坐标为 (x_0,y_0,z_0) ,北极点坐标为 (0,0,1) ,可以写出该直线的点向式方程:
\frac{x}{-x_0}=\frac{y}{-y_0}=\frac{z-1}{1-z_0}\\
再令 z=0 ,可以解得 \begin{cases} x = \frac{x_0}{1-z_0}\\ y = \frac{y_0}{1-z_0} \end{cases} ,于是复数 z=x+yi=\frac{x_0+y_0i}{1-z_0}(这里的z表示复数,前面的z表示笛卡尔坐标系下的z轴坐标分量),至此我们成功地用一个复数来表示了三维球面的坐标信息。
我们同样可以在已知一个复数的情况下,找到这个复数在球面上对应的笛卡尔坐标:
\begin{cases} x_0=\frac{z+\bar z}{2(|z|+1)}\\ y_0=\frac{z-\bar z}{2(|z|+1)i}\\ z_0= \frac{|z|}{1+|z|}\\ \end{cases}\\
<hr/>这里有一个很奇妙的反常识的现象,由于球面上除极点外的其他点都可以在复平面上找到一一对应的点,这表明一个面积有限的球面上的点数居然可以比无限延伸的平面上的点数还要多一个点。真是神奇啊~
参考
[1]钟玉泉《复变函数论》,高等教育出版社 第五版, |
|