2.1平面内的刚体运动

啊我

A.位姿表示
   开篇我们引入一个例子：



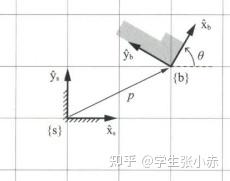
来自于-现代机器人学

  平面中我们选择一个固定坐标系{s}，单位坐标轴用\hat x_s与\hat y_s表示坐标轴的单位向量，在阴影物体上安装一个物体坐标系{b}，我们如何清晰的表达阴影物体的位姿？其实就是表达出{b}相对于{s}的关系。
  位置就是图中的向量p p=(p_x,p_y)表达了物体的位置，也可以使用p=p_x\hat x_s+p_y\hat x_s上式更加清晰的表达，并且反应出了向量p所在的参考坐标系。
  对于姿态，最简单的方法就是给定转角\theta，如图所示。还可以给出物体坐标系{b}中两个单位坐标轴相对固定坐标系{s}中两个单位坐标轴的方向，即\hat x_b=cos\theta \hat x_s + sin\theta \hat y_s\\\hat y_b=-sin\theta \hat x_s + cos\theta \hat y_s这是我们以后经常用的哦!   对于这个式子解释一下，当假想一个刚体在三维空间内做任意运动时，用单个转角\theta无法描述物体坐标系姿态，需要3个转角参数。对于这三个转角参数，使用上式用参考坐标系坐标轴表示物体坐标系坐标轴，就十分直观了。
  物体坐标系原点p写成向量形式p= \begin{bmatrix} p_x\\p_y \end{bmatrix}   单位向量x_by_b写成列向量形式，分解出矩阵[\hat x_b \ \hat y_b]=\begin{bmatrix} \hat x_s \ \hat y_s\end{bmatrix} * \begin{bmatrix}cos\theta & -sin\theta \\ sin\theta & cos\theta\\ \end{bmatrix}
  上式表明阴影物体姿态（物体坐标系单位轴）可使用基坐标单位轴通过矩阵P =  \begin{bmatrix}cos\theta & -sin\theta \\ sin\theta & cos\theta\\ \end{bmatrix}的作用后表示。矩阵P表示的是一个旋转矩阵，P有4个元素，不过有3个限制条件，两列是单位向量并且正交，这样只有一个单自由度参数\theta。
  我们组成(P,p)来描述\{b\}相对\{s\}的位姿。

田不辣和蜜三刀

LZ是天才，坚定完毕