|
|
\color{red} {Definition 7.1} 平面的坐标式参数方程(由平面上一点与平面的方位向量决定的平面)
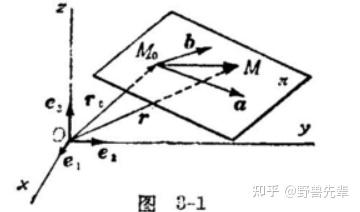
R^3 的仿射标架 \left\{ O;\ \overrightarrow{e_1},\overrightarrow{e_2},\overrightarrow{e_3} \right\} 中有一点 M_0\left( x_0,y_0,z_0 \right) ,两个不共线向量 \overrightarrow{a},\overrightarrow{b} 为平面 \pi 的方位向量(确定一个平面), \overrightarrow{M_0M}=\overrightarrow{r} -\overrightarrow{r_0} =u\overrightarrow{a}+v\overrightarrow{b},\ u,v\in R
令 \overrightarrow{r_0} =\left\{ x_0,y_0,z_0 \right\},\overrightarrow{r} =\left\{ x,y,z \right\},\overrightarrow{a} =\left\{ X_1,Y_1,Z_1 \right\},\overrightarrow{b} =\left\{ X_2,Y_2,Z_2 \right\}
有 \begin{cases}x=x_{0}+X_1u+X_{2}v,\\ y=\ y_{0}+Y_1u+Y_{2}v,\\ z=\ z_{0}+Z_{1}u+Z_{2}v.\end{cases}
\color{green} {Example7.1} 已知平面 \pi 的方程是 Ax+By+Cx+D=0 .两点 M_1(x_1,y_1,z_1) 和 M_2(x_2,y_2,z_2) 不在平面 \pi 上,已知连接 M_1 与 M_2 的直线 L .交平面 \pi 于点 M .求实数k的值,使得 \overrightarrow{M_1M}=k\overrightarrow{MM_2}
Sloution \because \overrightarrow{M_1M}=k\overrightarrow{MM_2}\ \ \ \ \therefore \overrightarrow{M_1M}=k(\overrightarrow{MM_1}+\overrightarrow{M_1M_2})\Rightarrow \overrightarrow{M_1M}=\frac{k}{1+k}\overrightarrow{M_1M_2}
\because M_1 和 M_2 不重合 \therefore k\ne -1 设 M(x,y,z) 推理得 x=\frac{1}{1+k}\left( x_1+kx_2 \right) ,y=\frac{1}{1+k}\left( y_1+ky_2 \right) ,z=\frac{1}{1+k}\left( z_1+kz_2 \right)
\therefore \frac{A}{1+k}\left( x_1+kx_2 \right) +\frac{B}{1+k}\left( y_1+ky_2 \right) +\frac{C}{1+k}\left( z_1+kz_2 \right) +D=0
\therefore k=-\frac{Ax_1+By_1+Cz_1+D}{Ax_2+By_2+Cz_2+D}
\color{red} {Definition 7.2} 平面的点位式方程
(\overrightarrow{r} -\overrightarrow{r_0} )\cdot (\overrightarrow{a}\times \overrightarrow{b})=(u\overrightarrow{a}+v\overrightarrow{b})\cdot (\overrightarrow{a}\times \overrightarrow{b})\Rightarrow (\overrightarrow{r} -\overrightarrow{r_0} ,\overrightarrow{a} ,\overrightarrow{b} )=0
\begin{vmatrix} x-x_0 & y-y_{0} & z-z_{0} \\ X_{1} & Y_{1} & Z_{1} \\ X_{2} & Y_{2} & Z_{2} \end{vmatrix}=0
\color{red} {Definition 7.3} 平面的三点式方程
令 \overrightarrow{a}=\overrightarrow{r_2}-\overrightarrow{r_1},\overrightarrow{b}=\overrightarrow{r_3}-\overrightarrow{r_1} ,得 (\overrightarrow{r} -\overrightarrow{r_1}, \overrightarrow{r_2} -\overrightarrow{r_1},\overrightarrow{r_3} -\overrightarrow{r_1} )=0
\begin{vmatrix} x & y & z & 1\\ x_1 & y_{1} &z_{1}&1 \\ x_2 & y_2 & z_2 &1 \\ x_3 & y_3 &z_3 & 1 \end{vmatrix}=0\Leftrightarrow \begin{vmatrix} x-x_1 & y-y_{1} & z-z_{1} \\ x_2-x_1 & y_2-y_{1} & z_2-z_{1} \\ x_3-x_1 & y_3-y_{1} & z_3-z_{1} \end{vmatrix}=0
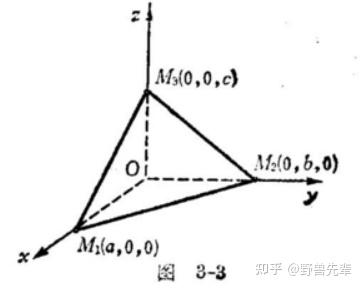
\color{red} {Definition 7.4} 平面的截距式方程
已知与坐标轴交点为 A(a,0,0),B(0,b,0),C(0,0,c) 的平面方程可写为 \frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1
\color{green} {Example7.2} 设从坐标原点到平面 \frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1 的距离为 p ,证明: \frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}=\frac{1}{p^2}
Proof 由 Definition7.7 已知,可令 \frac{1}{a}=\frac{cos\alpha}{p},\frac{1}{b}=\frac{cos\beta}{p},\frac{1}{c}=\frac{cos\gamma}{p} , \because {cos^2\alpha}+{cos^2\beta}+{cos^2\gamma}=1\ \ \ \ \therefore \frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}=\frac{1}{p^2}
\color{red} {Definition 7.5} 平面的一般方程
因为空间任一平面都可以用它上面的一点 M_0\left( x_0,y_0,z_0 \right) 和它的方位向量 \vec{a}=\left\{ X_1,Y_1,Z_1 \right\} ,\vec{b}=\left\{ X_2,Y_2,Z_2 \right\} 确定,因而任一平面都可以用点位式方程表示,把它展开就可写成
Ax+By+Cz+D=0 ,其中A=\left| \begin{matrix} Y_1& Z_1\\ Y_2& Z_2\\ \end{matrix} \right|, B=\left| \begin{matrix} Z_1& X_1\\ Z_2& X_2\\ \end{matrix} \right|, C=\left| \begin{matrix} X_1& Y_1\\ X_2& Y_2\\ \end{matrix} \right|, D=-\left| \begin{matrix} x_0& y_0& z_0\\ X_1& Y_1& Z_1\\ X_2& Y_2& Z_2\\ \end{matrix} \right|.
因为 \vec{a},\vec{b} 不共线,所以 A,B,C 不全为零,这表明空间任一平面都可以用关于 x,y,z 的三元一次方程来表示
此方程可改写成 \left| \begin{matrix} x+\frac{D}{A}& y& z\\ B& -A& 0\\ C& 0& -A\\ \end{matrix} \right|=0
\color{blue} {Theorem 7.1} 平面的方程都可表示成一不关于变量 x,y,z 的一次方程;反过来,每一个关于变量 x,y,z 的一次方程都表示一个平面
\color{green} {Example 7.3} 求过点 P_0\left( x_0,y_0,z_0 \right) 并且与平面 \pi :Ax+By+Cz +D=0 平行的平面 \sigma 的方程
Sloution 由 \pi 的方程 Ax+By+Cz+D=0 (不妨设 B≠0 )可得 \pi 的方位向量为 \left\{ B,-A,0 \right\} ,\left\{ 0,-C,B \right\} ,
\because \pi //\sigma , \therefore \pi 的方位矢量也是 \sigma 的方位向量,于是 \sigma 的方程为 \left| \begin{matrix} x-x_0& y-y_0& z-z_0\\ B& -A& 0\\ 0& -C& B\\ \end{matrix} \right|=0
展开得 AB\left( x-x_0 \right) +B^2\left( y-y_0 \right) +BC\left( z-z_0 \right) =0 ,即 Ax+By+Cz=Ax_0+By_0+Cz_0
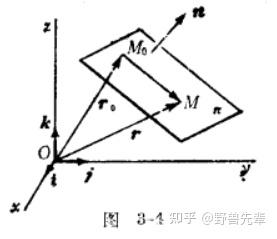
\color{red} {Definition 7.6} 平面的点法式方程
如果在空间给定一点 M_0 和一个非零向量 \overrightarrow{n} ,那么通过点 M_0 且与矢量 \overrightarrow{r_1} 垂直的平面也唯一地被确定。我们把与平面垂直的非零向量叫做平面的法向量或简称平面的法向量, \overrightarrow{OM_0}=\overrightarrow{r_0},\overrightarrow{MM_0}=\overrightarrow{r}-\overrightarrow{r_0} ,故 \overrightarrow{n}(\overrightarrow{r}-\overrightarrow{r_0})=\overrightarrow{0} ,有点法式方程 A\left( x-x_0 \right) +B\left( y-y_0 \right) +C\left( z-z_0 \right) =0
\color{green} {Example 7.4} 平面 \pi 通过三点M_1(3,-1,5),M_2(4,-1,1),M_3(2,0,2) ,求 \pi 的一个法向量和其点法式方程
Sloution \because \overrightarrow{M_1M_2}=\left\{ 1,0,-4 \right\},\overrightarrow{M_1M_3}=\left\{ -1,1,-3 \right\},\overrightarrow{M_1M_2}//\pi,\overrightarrow{M_1M_3}//\pi 且 \overrightarrow{M_1M_2} 不平行于 \overrightarrow{M_1M_3}
\therefore \pi 的一个法矢量为 \overrightarrow{M_1M_2}\times\overrightarrow{M_1M_3}=\left\{ -4,7,1 \right\} , \pi 的点法式方程为 4\left( x-2 \right) +7\left( y-0 \right) +\left( z-2 \right) =0
\color{red} {Definition 7.7} 平面的法式方程
将7.6中的向量单位化 \overrightarrow{n^0}=\frac{\overrightarrow{n}}{\left| \overrightarrow{n} \right|} ,取自原点 O 向平面所引垂线的垂足 P ,而x的法向量取单位法矢量n°,当平面不过原点时, \overrightarrow{n^0} 的正向取做与 \overrightarrow{OP} 相同(图35);当平面通过原点时, \overrightarrow{n^0} 的正向在垂直于平面的两个方向中任意取定一个,设 \left| \overrightarrow{OP} \right|=\overrightarrow{p} 那么点P的径矢 \overrightarrow{OP}=p\overrightarrow{n^0} ,改写得到的方程为 \overrightarrow{n^0}(\overrightarrow{r}-p\overrightarrow{n^0})=0,\overrightarrow{n^0}=\left\{ cos\alpha,cos\beta,cos\gamma \right\} ,得 xcos\alpha+ycos\beta+zcos\gamma-p=0
\color{green} {Example7.5} 把平面 \pi 的方程 3x-2y+6z+14=0 化为法式方程,求自原点指向平面 \pi 的单位法向量及其方向余弦,并求原点到平面 \pi 的距离
Sloution\ \because A=3,B=-2,C=6,D=14>0 ,取 \lambda=-\frac{1}{\sqrt{A^2+B^2+C^2}}=-\frac{1}{7}
得法式方程 -\frac{3}{7}x+\frac{2}{7}y-\frac{6}{7}z-2=0 ,原点指向平面 \pi 的单位法矢量为 \overrightarrow{n^0}=\left\{ -\frac{3}{7},\frac{2}{7},-\frac{6}{7} \right\} ,其方向余弦为 cos\alpha=-\frac{3}{7},cos\beta=\frac{2}{7},cos\gamma=-\frac{6}{7} ,原点到平面 \pi 的距离为 p=2
\color{red} {Definition 7.8} 点到平面的距离
一点到平面上的点之间的最短距离,叫做该点与平面之间的距离,记为 d(distance)
\color{red} {Definition 7.9} 离差
如果自点 M_0 到平面 \pi 引垂线,垂足为Q,那么向量 \overrightarrow{QM_0} 在平面 \pi 的单位法向量 \overrightarrow{n^0} 上的射影叫做点 M_0 与平面 \pi 间的离差,记为 \delta=injection_\overrightarrow{n^0}\overrightarrow{QM_0}
\color{purple} {Annotation } d=\left| \delta\right|
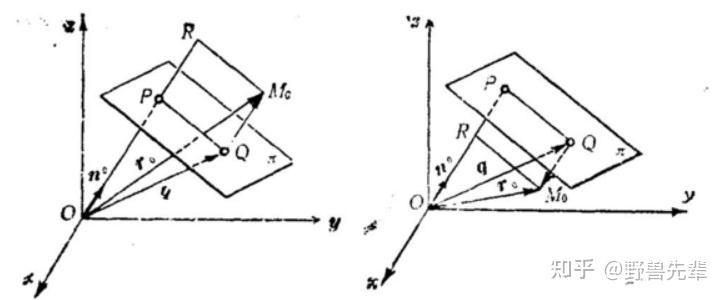
\color{blue} {Theorem 7.2} 点 M_0 与平面 \overrightarrow{n^0}\overrightarrow{r}-p=0 间的离差为 \delta=\overrightarrow{n^0}\overrightarrow{r_0}-p,\overrightarrow{r_0}=\overrightarrow{OM_0},p=\left| \overrightarrow{OP} \right|
Proof \delta=injection_\overrightarrow{n^0}\overrightarrow{QM_0}=\overrightarrow{n^0}\cdot\left( \overrightarrow{OM_0}-\overrightarrow{OQ} \right)=\overrightarrow{n^0}\cdot\left( \overrightarrow{r_0}-\overrightarrow{q} \right)
\because\overrightarrow{n^0}\cdot\overrightarrow{q}=p \therefore \delta=\overrightarrow{n^0}\overrightarrow{r_0}-p
\color{blue}{Corollary7.2.1} 点 M_0(x_0,y_0,z_0) 与平面 \overrightarrow{n^0}\overrightarrow{r}-p=0 间的离差为 \delta=x_0cos\alpha+y_0cos\beta+z_0cos\gamma-p
\color{blue}{Corollary7.2.2} 点 M_0(x_0,y_0,z_0) 与平面 Ax+By+Cz+D=0 间的离差为 \delta=\frac{Ax_0+By_0+Cz_0+D}{\sqrt{A^2+B^2+C^2}}
\color{blue}{Corollary7.2.3} 令 f\left( x,y,z \right) =Ax+By+Cz+D ,点 M_0(x_0,y_0,z_0) ,平面 \pi :Ax+By+Cz+D=0
f\left( x_0,y_0,z_0 \right) =0\Rightarrow M在平面 \pi 上
f\left( x_0,y_0,z_0 \right) >0\Rightarrow M在垂直于平面 \pi 向上的区域
f\left( x_0,y_0,z_0 \right) <0\Rightarrow M在垂直于平面 \pi 向下的区域
\color{green}{Example 7.6} 试求由平面 \pi_1:2x-y+2z-3 与 \pi_2:3x+2y-6z-1=0 所构成的二面角的角平分面的方程,在此二面角内有点 M(1,2-3)
Sloution 设角平分面上有一点 P(x&#39;,y&#39;,z&#39;) , P 到两平面的距离相同 \therefore d_1=\frac{\left| 2x-y+2z-3 \right|}{\sqrt{2^2+(-1)^2+2^2}}=\frac{\left| 3x+2y-6z-1 \right|}{\sqrt{3^2+2^2+(-6)^2}}=d_2
得到2个平面 \varphi_1:5x+3y-32z-19=0 和 \varphi_2:23x-y-4z-24=0
经检验, \varphi_2:23x-y-4z-24=0 满足条件
\color{blue} {Theorem 7.3} 平面 \pi_1:A_1x+B_1y+C_1z+D_1=0 和 \pi_2:A_2x+B_2y+C_2z+D_2=0 相交的充要条件为 A_1:B_1:C_1\ne A_2:B_2:C_2 ,平行的充要条件为 \frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2}\ne \frac{D_1}{D_2} ,重合的充要条件为 \frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2}= \frac{D_1}{D_2}
二面角 \angle(\pi_1,\pi_2)=\angle(\overrightarrow{n_1},\overrightarrow{n_2})\ \ or\ \ \pi-\angle(\overrightarrow{n_1},\overrightarrow{n_2})
cos\angle(\pi_1,\pi_2)=\pm cos\theta=\pm \frac{\overrightarrow{n_1}\cdot\overrightarrow{n_2}}{\left| \overrightarrow{n_1} \right|\left| \overrightarrow{n_2} \right|}=\pm \frac{A_1A_2+B_1B_2+C_1C_2}{\sqrt{A_{1}^{2}+B_{1}^{2}+C_{1}^{2}}\sqrt{A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}}
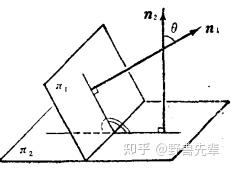
\color{blue} {Theorem 7.4} 两平面 \pi_1 和 \pi_2 互相垂直的充要条件为 A_1A_2+B_1B_2+C_1C_2=0
\color{red} {Definition 7.10} 由直线上一点与直线的方向所决定的直线方程
在空间给定了一点 M_0 与ー个非零向量 \overrightarrow{v} ,那么通过点 M_0 且与向量 \overrightarrow{v} 平行的直线 l 就唯一地被确定,向量 \overrightarrow{v} 叫做直线的方向向量。
\overrightarrow{M_0M}=\overrightarrow{r}-\overrightarrow{r_0}=t\overrightarrow{v} ,设 M_0(x_0,y_0,z_0),M(x,y,z) ,那么 \overrightarrow{r_0}=\left\{ x_0,y_0,z_0 \right\},\overrightarrow{r}=\left\{ x,y,z \right\} ,再设 \overrightarrow{v}=\left\{ X,Y,Z \right\} ,可得 \begin{cases} x=x_0+Xt\\ y=y_0+Yt\\ z=z_0+Zt\\ \end{cases} (坐标式参数方程)
消去参数t,得 \frac{x-x_0}{X}=\frac{y-y_0}{Y}=\frac{z-z_0}{Z} (直线的标准方程)
\color{red} {Definition 7.11} 两点式方程
通过空间两点 M_1(x_1,y_1,z_1) 和 M_2(x_2,y_2,z_2) 的直线 l 的方程 \frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}
\color{red} {Definition 7.12} 对称式方程
取单位向量 \overrightarrow{v^0}=\left\{ cos\alpha,cos\beta,cos\gamma \right\},\overrightarrow{r}=\overrightarrow{r_0}+t\overrightarrow{v^0} ,有对称式方程 \frac{x-x_0}{cos\alpha}=\frac{y-y_0}{cos\beta}=\frac{z-z_0}{cos\gamma} , cos\alpha=\pm\frac{l}{\sqrt{l^2+m^2+n^2}},cos\beta=\pm\frac{m}{\sqrt{l^2+m^2+n^2}},cos\gamma=\pm\frac{n}{\sqrt{l^2+m^2+n^2}}
\color{red} {Definition 7.13} 直线的一般方程
设有两个平面 \pi_1 和 \pi_2 的方程为 \left. \begin{array}{r} \pi _1: A_1x+B_1y+C_1z+D_1=0\\ \pi _2: A_2x+B_2y+C_2z+D_2=0\\ \end{array} \right\} ,它的一个方向向量为 \left| \begin{matrix} B_1& C_1\\ B_2& C_2\\ \end{matrix} \right|:\left| \begin{matrix} C_1& A_1\\ C_2& A_2\\ \end{matrix} \right|:\left| \begin{matrix} A_1& B_1\\ A_2& B_2\\ \end{matrix} \right|
化为标准方程就是 \frac{x-x_0}{\left| \begin{matrix} B_1& C_1\\ B_2& C_2\\ \end{matrix} \right|}=\frac{y-y_0}{\left| \begin{matrix} C_1& A_1\\ C_2& A_2\\ \end{matrix} \right|}=\frac{z-z_0}{\left| \begin{matrix} A_1& B_1\\ A_2& B_2\\ \end{matrix} \right|} ( (x_0,y_0,z_0) 为直线上一点)
\color{blue} {Theorem 7.5} xOz 平面与 yOz 平面射影式方程: \begin{cases} x=\frac{\left| \begin{matrix} B_1& C_1\\ B_2& C_2\\ \end{matrix} \right|}{\left| \begin{matrix} A_1& B_1\\ A_2& B_2\\ \end{matrix} \right|}z+\frac{\left| \begin{matrix} B_1& D_1\\ B_2& D_2\\ \end{matrix} \right|}{\left| \begin{matrix} A_1& B_1\\ A_2& B_2\\ \end{matrix} \right|}\\ y=\frac{\left| \begin{matrix} C_1& A_1\\ C_2& A_2\\ \end{matrix} \right|}{\left| \begin{matrix} A_1& B_1\\ A_2& B_2\\ \end{matrix} \right|}z+\frac{\left| \begin{matrix} D_1& A_1\\ D_2& A_2\\ \end{matrix} \right|}{\left| \begin{matrix} A_1& B_1\\ A_2& B_2\\ \end{matrix} \right|}\\ \end{cases}
\color{green}{Example 7.7}

\color{blue} {Theorem 7.6}

\color{blue} {Theorem 7.7} 直线 l 与平面 \pi 的相关位置
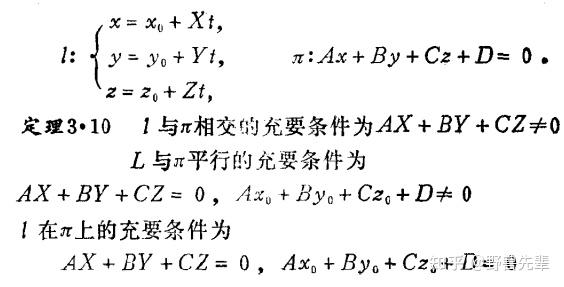
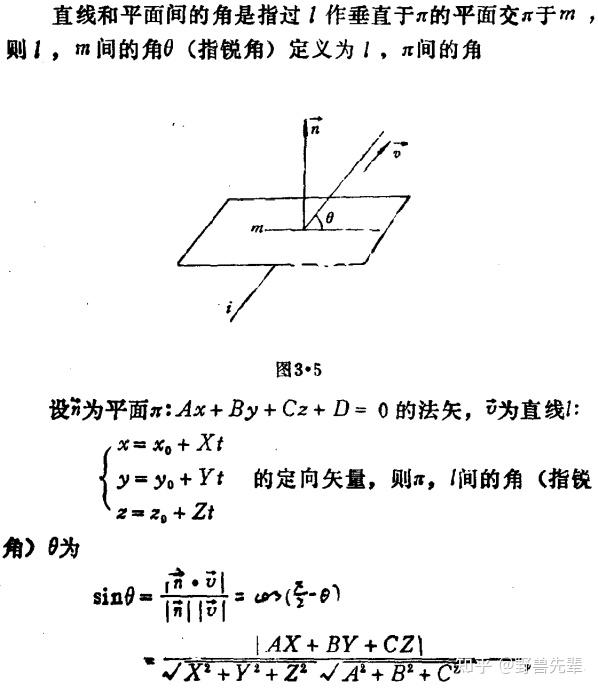
\color{blue} {Theorem 7.8} 直线与平面的夹角

\color{blue} {Theorem 7.9} 直线与空间中的点的相关位置

\color{green}{Example 7.8}

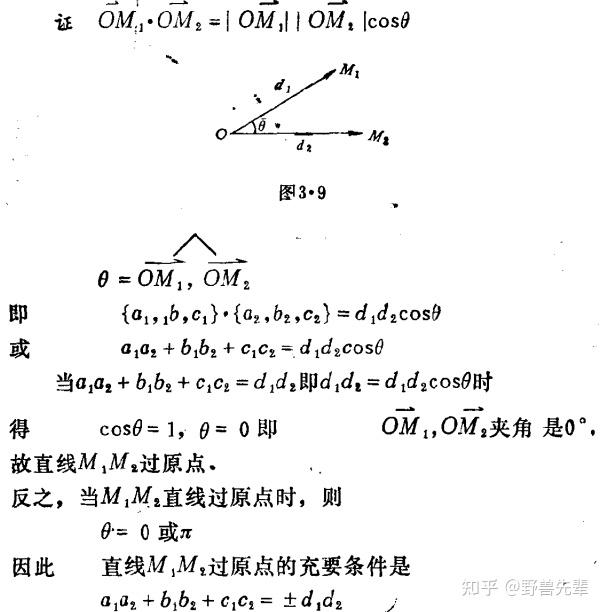
\color{blue} {Theorem 7.10} 空间两直线的相关位置

\color{blue} {Theorem 7.11} 空间两直线的夹角

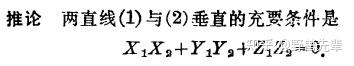
\color{red} {Definition 7.13} 空间两直线上的点之间的最短距离叫做这两条直钱之间的距离
\color{red} {Definition 7.14} 与两条异面直线都垂直相交的直线叫做两异面直线的公垂线,两异面直线间的距离显然就等于它们的公垂线夹于两异面直线间的线段的长
\color{blue} {Theorem 7.12} 异面直线之间的距离
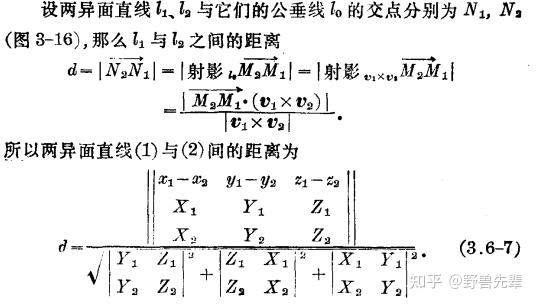
\color{blue} {Theorem 7.13} 直线 l_1:\frac{x-x_1}{X_1}=\frac{y-y_1}{Y_1}=\frac{z-z_1}{Z_1} 与直线 l_22:\frac{x-x_2}{X_2}=\frac{y-y_2}{Y_2}=\frac{z-z_2}{Z_2}
的公垂线方程为
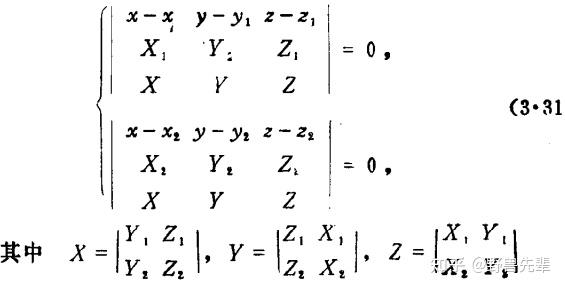
\color{orange} {Conclusion1}

\color{orange} {Conclusion2}

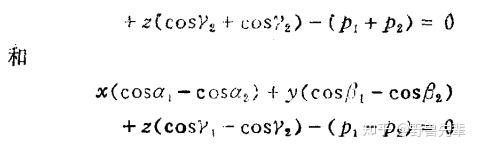
\color{green}{Example 7.9}

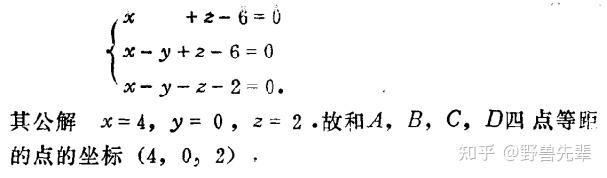
\color{red} {Definition 7.15} 空间中通过同一条直线的所有平面的集合叫做有轴平画束,那条直线叫做平面束的轴
\color{red} {Definition 7.16} 空间中平行于同一个平面的所有平面的集合叫做平行平面束
\color{blue} {Theorem 7.14} 如果两个平面 \pi_1:A_1x+B_1y+C_1z+D_1=0,\pi_2:A_2x+B_2y+C_2z+D_2=0 交于一条直线 l ,那么以直线 l 为轴的有轴平面東的方程是: l(A_1x+B_1y+C_1z+D_1)+m(A_2x+B_2y+C_2z+D_2)=0 , l,m 是不全为0的任意实数

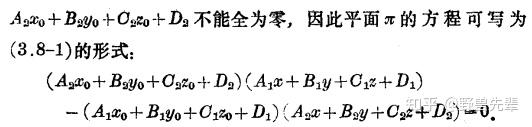
\color{blue} {Theorem 7.15}

\color{blue}{Corollary7.15.1}
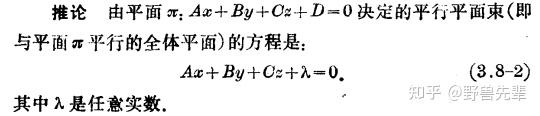
\color{blue}{Corollary7.15.2}


\color{blue}{Corollary7.15.3} 直线的一般方程为 \begin{cases} A_1x+B_1y+C_1z+D_1=0\\ A_2x+B_2y+C_2z+D_2=0\\ \end{cases} ,平面的一般方程为 Ex+Fy+Gz+H=0 ,过直线的平面束为 (A_1x+B_1y+C_1z+D_1)+\lambda(A_2x+B_2y+C_2z+D_2)=0 ,直线投影到平面上后的方程为 \begin{cases} Ex+Fy+Gz+H=0\\ \left( A_1+A_2\lambda \right) x+\left( B_1+B_2\lambda \right) y+\left( C_1+C_2\lambda \right) z+\left( D_1+D_2\lambda \right) =0\\ \end{cases} ,其中 \lambda =-\frac{A_1E+B_1F+C_1G}{A_2E+B_2F+C_2G}
\color{green}{Example 7.10}

\color{green}{Example 7.11}

 |
|