|
|
超平面的公式
首先明确几个定义：(1) 超平面是指n维线性空间中维度为n-1的子空间。它可以把线性空间分割成不相交的两部分。比如二维空间中，一条直线是一维的，它把平面分成了两块；三维空间中，一个平面是二维的，它把空间分成了两块。(2) 法向量是指垂直于超平面的向量。
在 \mathbb{R}^3 空间中，假如有法向量 \omega ，过原点的平面内任意原点出发的向量 x 必然与之满足 w^Tx=0 。如果平面沿着法向量的方向上下平移了，那么这个方程就不成立了。
我们假设平移之后平面经过 x'(x_1',x_2',x_3') ，平面内任意一点记为 x(x_1,x_2,x_3) ，法向量记为 \omega(\omega_1,\omega_2,\omega_3) ，如下图。
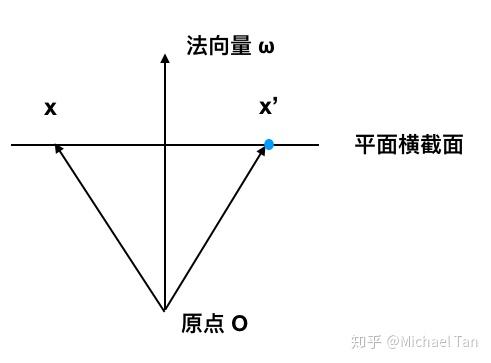
不难看出， x-x' 在平面内，当然也就和法向量垂直。于是我们有：
(x-x')w=0
(x_1-x_1', x_2-x_2',x_3-x_3')\cdot(\omega_1,\omega_2,\omega_3)=0
化简后得：
x_1\omega_1+x_2\omega_2+x_3\omega_3=\omega_1x_1'+\omega_2x_2'+\omega_3x_3'
。即 \omega^Tx=\omega^Tx' 。由于其为常数项，令 b=-\omega^Tx' ，于是超平面的公式可以写成：
\omega^Tx+b=0
1. 这个结论同样适用于 R^n 空间； 2. 无论超平面如何平移，系数始终是法向量 \omega 。
点到超平面的距离
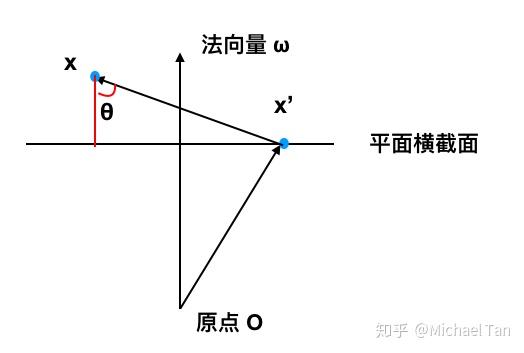
上图中 x 是平面外的一点。我们要求的距离记为 d ，也就是红色的线段。根据三角函数可以得到： \cos{\theta}=\dfrac{d}{||x-x'||} （空间中一点向超平面作垂线， \theta 只能是锐角，不必担心正负）。因为 d 肯定和法向量平行，所以这样来算夹角： |(x-x')\omega|=||x-x'||\cdot||\omega||\cdot\cos{\theta} （因为法向量可能反向，所以给等式左边加上绝对值），联立得：
d = \dfrac{|(x-x')\omega|}{||\omega||}=\dfrac{|\omega x-\omega x'|}{||\omega||}
因为 x' 在超平面内， \omega x'=-b ，于是最后得到的任意点到超平面的距离公式：
d=\dfrac{|\omega x+b|}{||\omega||}
本推导过程主要是方便我个人理解，在此分享，如有疏漏，不吝赐教。 |
|
发表于 2023-3-11 19:04:10